DIAGRAMAS DE KARNAUGH

DIAGRAMAS DE KARNAUGH
Es un metodo grafico que se utiliza para simplificar circuitos lógicos en un proceso simple y ordenado. Es metodo que se basa en los teoremas booleanos estudiados anteriormente y su utilidad practica se limita a 5 variables. Las reglas a seguir son las siguientes:

    • A partir de la tabla de verdad sacar las expresiones booleanas en forma de minterns o maxterms.
    • Colocar los 1 corespondientes en el diagrama por cada grupo de variables operadas por AND si es en forma de minterns u operadas por OR si es en forma de maxterms.
    • Agrupar los 1 adyacentes (las agrupaciones se realizan en grupos de 2, 4, 8 1)
    • Eliminar las variables que aparezcan con su complemento.
    • Enlazamos con OR los resultados obtenidos (si es en forma de minterns) o con AND (si es en forma de maxterms).
Tomemos la tabla de verdad 5. Lo primero que debemos hacer es sacar las expresiones booleanas correspondientes:



A
B
Q
0
0
0
0
0
1
A·B
1
0
1
A·B
1
1
1
A·B
Q=(A·B)+(A·B)+(A·B)
Tabla 5


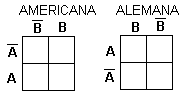
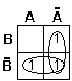
Luego procedemos a colocar cada 1 correspondiente en el diagrama por cada grupo de variables operadas con AND (para nuestro ejemplo). Los diagramas de Karnaugh pueden presentarse de dos maneras diferentes: la americana y la alemana, demos un vistazo a dichas presentaciones:



Figura 7: Diagramas de Karnaugh para 2 variables


Figura 8: Diagramas de Karnaugh para 3 variables


Figura 9: Diagramas de Karnaugh para 4 variables


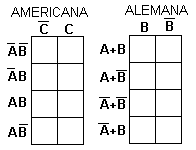
Ahora que conocemos las maneras en que se pueden presentar las diagramas procedemos a colocar los 1 correspondientes por cada grupo de variables operadas con AND (en nuestro ejemplo)



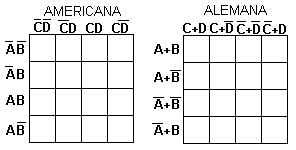
Figura 10: Colocación de los unos en el mapa de Karnaugh



Luego procedemos a agrupar los 1 adyacentes que se encuentren en el diagrama, estas agrupaciones se realizan en grupos de 2, 4, o de 8 "1" . Debemos tratar en lo posible de no realizar tantas agrupaciones.



Figura 11: Agrupación de términos

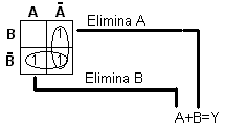
Despues de realizar las agrupaciones eliminanos por cada grupo las variables que aparezcan con su complemento. En el agrupamiento de 2 "1" se elimina una variable; en el agrupamiento de 4 "1" se eliminan 2 variables y en el agrupamiento de 8 "1" se eliminan 3 variables.



Figura 12: Eliminación de términos


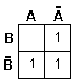
Por ultimo enlazamos con OR (ya que nuestro ejemplo es en forma de minterns) los resultados que obtuvimos de la eliminación de variables.

Q = A +B

De esta manera la ecuacion logica Q=(A·B)+(A·B)+(A·B) nos quedaría reducida a una puerta OR