SIMPLIFICACION DE CIRCUITOS LÓGICOS :
Una vez que se obtiene la expresión booleana para un circuito lógico, podemos reducirla a una forma más simple que contenga menos términos, la nueva expresión puede utilizarse para implantar un circuito que sea equivalente al original pero que contenga menos compuertas y conexiones.
El álgebra booleana (Algebra de los circuitos lógicos tiene muchas leyes o teoremas muy útiles tales como :
1. Ley de Morgan :
- 1. A + B = A·B
2. A·B = A + B
2. Ley Distributiva :
- 3. A+(B·C) = (A+B)·(A+C)
4. A·(B+C) = A·B+A·C
Ademas de las leyes formales para las funciones AND y OR :
- 5. A·0 = 0 ; A+0 = A
6. A·1 = A ; A+1 = 1
7. A·A = A ; A+A = A
8. A·A = 0 ; A+A = 1
y la Ley de la Involución:
- 9. A(negada) = A
Considerar la expresión booleana A·B + A·B + A·B = Y, un diagrama lógico de ésta expresión aparece en la Figura 1. Observar que deben utilizarse seis puertas para implementar este circuito lógico, que realiza la lógica detallada en la tabla de verdad (Tabla 1)
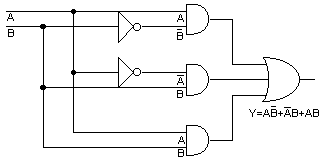
Figura 1: Circuito lógico no simplificado
| ENTRADAS | SALIDA | ||
| B | A | Y | |
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 | |
![]()
Figura 2: Circuito lógico simplificado
Aplicando el álgebra booleana :
A·B + A·B + A·B = Y
RAZONES
= A·B + (A·B + A·B) , Propiedad asociativa
= A·B + B·(A+A) , 4. [A·(B + C) = A·B + A·C]
= A·B + B·1 , 8. [A + A = 1]
= A·B + B , 6. [B·1 = B]
= B + A·B , Propiedad conmutativa
= (B + A)·(B + B) , 3. [A + (B·C) = (A + B)·(A + C)]
= (B + A)·1 , 8. [A + A = 1]
= B + A , 6. [A * 1 = A]
Concluimos entonces que una sola puerta OR de dos entradas realiza la misma función (¡ De hecho la tabla 1 corresponde a la función OR !)