LA PUERTA OR EXCLUSIVA ó XOR
La OR - exclusiva se denomina la puerta de << algunos pero no todos >>. El termino OR - exclusiva con frecuencia se sustituye por XOR. La tabla de verdad para la función XOR se muestra en la tabla 10 . un cuidadoso examen muestra que esta tabla de verdad es similar a la tabla de verdad OR, excepto que cuando ambas entradas son 1 la puerta XOR genera un 0.
| XOR | |||
0 1 1 |
1 0 1 |
1 1 1 |
1 1 0 |
La operación de una puerta XOR es análoga a la del circuito eléctrico mostrado en la fig. 18. los interruptores A y B simulan las entradas y la lampara (Y) la salida .
Figura 18: Circuito eléctrico equivalente de una compuerta XOR
Los interruptores A y B están acoplados mecánicamente a los interruptores A y B de modo que cuando A se cierra entonces A se abre y viceversa . lo mismo puede decirse del interruptor B con respecto al B.
Cuando los interruptores A y B están ambos cerrados o ambos abiertos la lampara no enciende. En cambio , cuando uno de ellos , por ejemplo el A , esta abierto y el otro, B, esta cerrado , entonces la lampara se enciende.
Una booleana para la puerta XOR puede obtenerse de la tabla de verdad la fig. 19 la expresión es A ·B + Å · B = Y a partir de esta expresión booleana puede construirse un circuito lógico utilizando puertas AND, puertas OR e inversores dicho circuito aparece en la fig. 19 a este circuito lógico realiza la función lógica XOR.
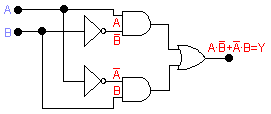
Figura 19: Circuito lógico que realiza la función XOR
El símbolo lógico convencional para la puerta XOR se muestra en la fig. 20 la expresión booleana A Å B, es una expresión XOR simplificada . el símbolo Å significa la función XOR en álgebra booleana. Se dice que las entradas A y B de la fig. 20 realiza la función OR - exclusiva.
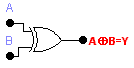
Figura 20: Símbolo lógico de una compuerta XOR