Figura 6: Circuito equivalente de una compuerta OR
La puerta OR se denomina y la puerta de << cualquiera o todo >>.
El esquema de la figura 6 nos muestra la idea de la puerta OR, en el cual los interruptores han sido conectados en paralelo. El encendido de la lámpara se producirá si se cierra cualquiera de los dos interruptores o ambos.
Todas las posibles combinaciones de los interruptores se muestran en la tabla 4.
La tabla de verdad detalla la función OR del circuito de interruptores y lámpara.
| Interruptores de entrada | Luz de salida | |
| A | B | Y |
| Abierto
Abierto Cerrado Cerrado |
Abierto
Cerrado Abierto Cerrado |
Apagado
Encendido Encendido Encendido |
La tabla de la 4 describe el funcionamiento del circuito. Observamos, que de las 4 posibles combinaciones de cierre y apertura de los interruptores, 3 de ellas producen el encendido de la lampara , y de nuevo utilizando la convención de representar la condición cerrado o encendido por un 1 y la de abierto o apagado por un 0, se obtiene la tabla de verdad de la tabla 5.
Tabla 5: Tabla de verdad de una compuerta OR de dos entradas| A | B | Y |
| 0
0 1 1 |
0
1 0 1 |
0
1 1 1 |
El símbolo lógico estándar para la puerta OR esta dibujado en la fig. 7. observar la forma diferente de la puerta OR. La expresión booleana abreviada para esta función OR es A + B = Y observar que símbolo + significa OR en álgebra booleana . la expresión ( A+ B = Y ) se lee A OR B igual a salida Y .
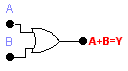
Figura 7: Símbolo de una compuerta OR
La expresión booleana , símbolo y tabla de verdad de una puerta OR de tres entradas o variables están dibujadas en las figuras 8, 9, y en tabla 6.
A + B + C = Y
Figura 8: Expresión booleana para una compuerta OR de tres entradas
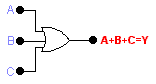
Figura 9: Compuerta OR de tres entradas
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |